Моделирование мыслительных процессов

Статья Виктора Михайловича Глушкова из книги «Кибернетика. Вопросы теории и практики», 1986 год. Эта же статья есть в журнале «Природа», №2, 1963 год. Рисунки взяты из журнальной версии.

Моделирование сложных мыслительных процессов – одна из самых увлекательных и вместе с тем самых сложных проблем кибернетики. Интерес к этой проблеме вызван двумя обстоятельствами. Во-первых, переход от простого наблюдения работы мыслительного аппарата человека к его активному моделированию позволит гораздо быстрее раскрыть многие тайны, окутывающие и по сей день процесс мышления. Во-вторых, моделирование мыслительных процессов с привлечением современной кибернетической техники служит основой для автоматизации многих видов умственной деятельности человека.

МОДЕЛЬ МОЗГА

В зависимости от целей, которые преследует моделирование мыслительных процессов, оно может осуществляться разными путями. Различают два основных вида такого моделирования – прямое и косвенное, или феноменологическое.

При прямом моделировании основное внимание уделяется естественному мыслительному аппарату – мозгу человека. Моделирование собственно мыслительных процессов получается при этом как результат моделирования этого аппарата. При косвенном моделировании воспроизводится лишь общий ход течения мыслительного процесса – закономерности перехода от одной мысли к другой. Что же касается способов реализации (внутреннего механизма) таких переходов, то они, как правило, имеют при этом мало общего с действительными процессами, протекающими в мозгу человека.

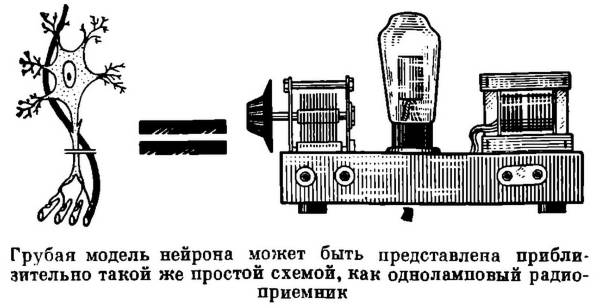
Биологов, изучающих мыслительный аппарат человека, разумеется, должен интересовать в первую очередь прямой метод моделирования. К сожалению, возможности этого метода в настоящее время весьма ограничены. Дело в том, что информационная модель нейрона, учитывающая многие известные в настоящее время тонкости его поведения, требует для своей реализации достаточно сложных радиоэлектронных схем. Огрубляя модель, удаётся снизить сложность соответствующих схем, однако при современном состоянии радиоэлектроники подобное снижение возможно лишь до известного предела. Для приблизительной ориентировки можно считать, что самая грубая модель нейрона имеет такой же порядок сложности, как одноламповый радиоприёмник. Но при уточнении модели сложность этих схем более уместно сравнивать со сложностью современных многоламповых приёмников и телевизоров. Разумеется, заменяя лампы полупроводниковыми или магнитными элементами, можно существенно уменьшить габариты схем, моделирующих нейроны, однако их сложность (измеряемая количеством используемых в схеме деталей) при этом сохраняет прежний порядок. Относительно высокой остаётся и стоимость подобного рода моделей. А ведь человеческий мозг состоит не менее чем из десяти миллиардов нейронов! Если стоимость модели одного нейрона принять равной всего 10 коп., то лишь на моделирование всех составляющих его нейронов пришлось бы затратить миллиард рублей! А ведь в эту сумму не входят ещё расходы на сборку и отладку схемы, которые, по-видимому, были бы ещё более грандиозными! К тому же в настоящее время далеко не ясно, каким образом должны быть соединены между собой модели нейронов, чтобы образовать систему, действительно моделирующую мозг.

Таким образом, правильно будет, если скажем, что при современном состоянии науки и техники задача прямого моделирования человеческого мозга практически неосуществима. Ещё очень многого нужно достигнуть в изучении строения мозга и в создании принципиально новых методов изготовления и монтажа радиоэлектронных элементов, чтобы осуществить моделирование этого сложнейшего и совершеннейшего живого органа. Пока же приходится ограничиваться гораздо более скромными целями, моделируя системы нейронов, состоящие из нескольких десятков или, в лучшем случае, из нескольких сот нейронов.

Следует, однако, отметить, что уже такое, весьма скромное по своим масштабам моделирование может принести большую пользу биологам, изучающим мозг и происходящие в нем процессы на клеточном уровне. Используя модель системы нейронов, биолог может проверять гипотезы, касающиеся закономерностей передачи информации от нейрона к нейрону в различных участках мозга, более детально изучать механизм возникновения и угасания условных рефлексов и т. д.

Серьёзное препятствие на пути широкого использования биологами методов электронного моделирования нейронов и систем нейронов – относительно высокая стоимость соответствующего электронного оборудования и необходимость специального персонала для его эксплуатации, ремонта и наладки. Однако в настоящее время эти препятствия можно легко преодолеть, используя универсальные электронные цифровые машины, установленные в вычислительных центрах или в научно-исследовательских институтах. Дело в том, что функционирование любой модели (не только мозга, но и какого угодно другого объекта) можно имитировать при помощи универсальной цифровой машины, составив и введя в неё соответствующую программу. В эту программу входит цифровое описание модели и условий, в которых она находится, а машина описывает поведение этой модели. От экспериментатора требуется лишь умение составить программу. Искусство программирования вопреки мнению, бытующему среди далёких от математики людей, вовсе не является чем-то непостижимо сложным. Любой человек, имеющий среднее образование, может при желании за несколько месяцев научиться хорошо программировать.

Научившись же этому, экспериментатор получает возможность легко подготовлять и проводить на универсальных цифровых машинах эксперименты со столь сложными моделями, каких ему никогда не удалось бы создать своими руками. Расходы при таком подходе к моделированию сводятся, по существу, лишь к оплате машинного времени и не идут ни в какое сравнение с затратами на изготовление аппаратуры, сходной по функциям с моделируемым органом.

К сожалению, биологи всё ещё крайне недостаточно используют новую мощную технику эксперимента, которая создана благодаря успехам современной кибернетики и вычислительной техники. В частности, немногочисленны пока и попытки моделирования на универсальных цифровых машинах отдельных нейронов и систем нейронов, хотя уже первые, пока ещё робкие эксперименты, показывают большие возможности, открывающиеся на этом пути. В качестве примеров успешного использования современных электронных вычислительных машин для моделирования элементов мыслительного аппарата человека можно указать следующие факты: в США изучалось поведение системы из нескольких сот связанных между собой относительно грубых моделей нейронов. Недавно на одной из вычислительных машин Института кибернетики в Киеве было осуществлено моделирование хотя и одного нейрона, но зато с учётом многих тонкостей его поведения.

Несмотря на огромную принципиальную важность прямого моделирования мыслительного аппарата человека, необходимо отметить, что основой для реальной автоматизации мыслительных процессов в настоящее время могут служить не прямые, а косвенные методы. Причину этого обстоятельства нетрудно понять, если вспомнить, что прямое моделирование, даже при условии использования электронных цифровых машин, может охватить пока элементы, состоящие из нескольких сот или в крайнем случае из нескольких тысяч нейронов. Всякий же сколько-нибудь сложный вид умственной деятельности человека использует одновременно гораздо большее число нейронов головного мозга. Да и обязательно ли нужно при автоматизации сложных мыслительных процессов слепо следовать естественному мыслительному аппарату – мозгу человека? История техники знает немало примеров, когда слепое копирование природы не только не двигало вперёд технику, но зачастую и тормозило её развитие. Достаточно вспомнить, что первые паровозы пытались снабдить «ногами», а на заре авиации много сил и энергии отняли попытки подражать маховым движениям крыльев птиц. Не следует забывать, что материальная основа сегодняшнего моделирования мыслительных процессов – электронные элементы – качественно отлична от материальной основы живых нейронов – живого белка. Механизм же моделирования должен отражать в первую очередь специфику его материальной основы. Те формы организации взаимных связей и передачи информации, которые хороши для живых нейронов, вовсе не обязаны быть хорошими для моделирующих их электронных элементов, и наоборот.

АЛГОРИТМ И КОДИРОВАНИЕ

На современном этапе развития кибернетики особое значение приобрели формы автоматизации различных участков умственной деятельности человека, основанные на их так называемом алгоритмическом описании. Понятие алгоритма, возникшее первоначально в математике, приобрело в настоящее время гораздо более универсальное значение. Алгоритмом называют любую конечную систему правил, позволяющих производить однозначное преобразование информации, заданной в обобщённой буквенной форме. Добавление термина «обобщённая» применительно к буквенной информации означает, что речь идёт не обязательно о буквах, латинского или какого-нибудь другого применяемого для записи лексической информации алфавита. В общей теории алгоритмов рассматриваются обобщённые алфавиты, состоящие из любых индивидуально различимых знаков или символов. Существенно лишь, чтобы общее число различных знаков, составляющих алфавит, было конечным.

Благодаря столь широкому толкованию понятия алфавита, любой вид информации, с которым человек встречается на практике, может быть представлен в (обобщённой) буквенной форме. Процесс такого представления называется обычно кодированием. Термин «кодирование» (или «перекодирование») относят также и к процессу перезаписи при помощи какого-либо алфавита информации, заданной первоначально в одном определённом алфавите.

При кодировании, как правило, стремятся пользоваться алфавитами с относительно небольшим числом букв. Например, поскольку общее число различных позиций на шахматной доске конечно, можно было бы кодировать каждую позицию специально отведённым для неё символом – обобщённой буквой. Однако алфавит при этом был бы чудовищно велик. Поэтому на практике, как известно, предпочитают кодировать шахматные позиции при помощи алфавита, состоящего из части букв латинского и русского алфавитов и восьми цифр (от 1 до 8).

Другой пример. Составляя рисунки заданного формата из черных и белых квадратиков фиксированного размера, можно получить конечное (хотя обычно и очень большое) число различных рисунков. Однако кодирование рисунков, использующее отдельную букву для каждого рисунка, практически неосуществимо (если только буквами не считать сами рисунки!). Более целесообразно поэтому ввести лишь две различные буквы для обозначения чёрного и белого квадратиков и кодировать рисунки последовательностями, составленными из этих букв (необходимо, разумеется, предварительно фиксировать порядок обегания рисунка, например, обегание по строкам или по столбцам).

При кодировании информации в обобщённых алфавитах возникают обобщённые слова, т. е. конечные последовательности обобщённых букв. Поскольку знак раздела между словами может быть включён в обобщённый алфавит, то любую конечную последовательность обобщённых слов можно считать одним словом. Так обычно и поступают в общей теории алгоритмов. Для целей же более естественного моделирования мыслительных процессов целесообразнее представлять себе информацию записанной в виде совокупности отдельных слов.

Имея в виду общность понятия алфавита, фактически любой вид умственной деятельности человека можно представить в виде преобразования буквенной информации. Если при этом к одной и той же входной информации человек всегда относит одну и ту же выходную информацию, а процесс преобразования входной информации в выходную описывается конечным (хотя, быть может, и очень большим) числом правил, то мы имеем дело с алгоритмом.

Пусть, например, мы имеем дело с шахматной игрой, входная информация представляет собой позицию перед очередным ходом, а выходная информация – позицию после выполнения этого хода. Легко понять, что одни лишь правила шахматной игры сами по себе не составляют алгоритма, поскольку они не определяют вообще говоря, однозначным образом очередной ход. Однако если дополнить эти правила специальными правилами, позволяющими оценивать различные позиции и выбирать каждый раз наилучший (с точки зрения данной системы правил) ход, то мы получим некоторый алгоритм игры в шахматы. Ясно, что существует не один, а много различных шахматных алгоритмов. Относительно нетрудно строить алгоритмы, моделирующие игру шахматистов низкой и даже средней квалификации. Гораздо труднее описать правила для моделирования игры сильных шахматистов. Эта проблема привлекает в настоящее время внимание целого ряда математиков (особенно в США) и, по-видимому, будет решена в ближайшие годы.

Что же даст алгоритмизация того или иного вида умственной деятельности? Оказывается, что на современном уровне развития кибернетики алгоритмическое описание мысленного процесса даёт, как правило, возможность его моделировать и автоматизировать на базе уже существующих универсальных электронных цифровых машин.

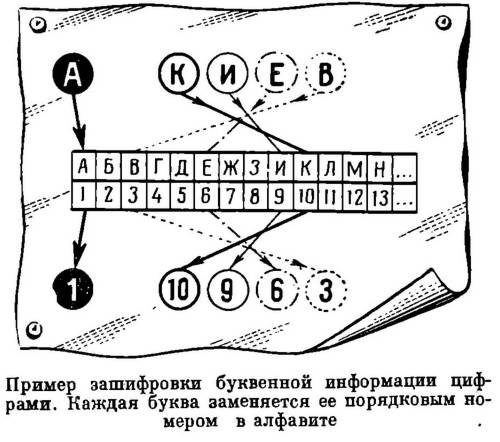
Дело в том, что любую буквенную информацию нетрудно закодировать цифрами (для этого достаточно, например, заменить каждую букву её порядковым номером в алфавите). После же этого любой алгоритм можно запрограммировать, т. е. записать в виде некоторой последовательности команд, выполняемых электронной цифровой машиной. Введя указанную последовательность (так называемую программу) в машину, мы заставляем её реализовать исходный алгоритм.

Если первый этап автоматизации – алгоритмическое описание процесса – выполнен достаточно тщательно, то второй этап (программирование) представляет собою уже чисто техническую работу, хотя, быть может, и весьма громоздкую. Критерием, позволяющим судить о тщательности выполнения алгоритмического описания, может служить следующий контрольный опыт: если человек, совершенно незнакомый с алгоритмируемым процессом (например, не умеющий играть в шахматы), может без всякой подготовки, руководствуясь лишь описанной системой правил (пусть очень медленно), выполнять этот процесс, то этап алгоритмирования может считаться выполненным удовлетворительно, а соответствующая система правил – подготовленной к программированию. Природа же указанных правил может быть любой: наравне с математическими формулами годятся правила, сформулированные подобно правилам грамматики или правилам уличного движения. Важно лишь, чтобы при пользовании этими правилами не возникало никаких двусмысленностей или неясностей (чего, например, о современных правилах уличного движения полностью сказать нельзя).

ВОЗМОЖНА ЛИ АВТОМАТИЗАЦИЯ НАУЧНОГО ТВОРЧЕСТВА?

Эффект автоматизации мыслительных процессов определяется прежде всего огромной скоростью и точностью работы современных электронных цифровых машин. Именно благодаря преимуществу в скорости машина оказывается способной выполнять соответствующую работу лучше, чем человек, составивший для неё программу. Например, при игре в шахматы, благодаря тому, что машина способна просматривать в единицу времени гораздо большее число вариантов, чем человек, она может регулярно обыгрывать составителя введённой в неё шахматной программы.

Возникающий подобным образом эффект кажущегося интеллектуального превосходства машины над человеком даёт возможность не просто автоматизировать ту или иную сферу умственной деятельности человека, но и резко поднять производительность труда в этой сфере. Необходимость же в подобном росте производительности труда ощущается сегодня в целом ряде областей умственной деятельности.

Общеизвестными примерами являются научные и инженерные расчёты, техническое проектирование, планирование народного хозяйства, оптимальное управление производственными процессами, диспетчерская и информационная служба. В настоящей статье мы остановимся на другом примере, а именно на проблеме автоматизации научного творчества.

Речь идёт не об автоматизации вспомогательных работ, сопутствующих почти каждому научному исследованию, как, например, выполнение трудоёмких расчётов (это успешно делается уже сегодня), поиск и реферирование необходимой литературы (методы автоматизации участка работы успешно разрабатываются и найдут применение в ближайшем будущем). Нас же интересует сам процесс научного творчества и в первую очередь – в области точных наук (математики, физики и т. д.).

В качестве примера рассмотрим математику. Процесс научного творчества здесь многогранен. Он включает введение новых понятий, постановку новых проблем, доказательство теорем, построение примеров и контрпримеров и т. д. Выделим из перечисленных задач лишь одну, а именно доказательство (или опровержение) уже сформулированных теорем. Существует широко распространённое мнение, что именно эта задача составляет основу научного творчества в области математики. Трудоёмкость и сложность этой задачи в общем случае несомненна; если не считать времени, затрачиваемого на ознакомление с литературой, то поиски доказательства или опровержения теорем занимают львиную долю в бюджете времени каждого математика. Существуют примеры, когда на поиски доказательства одной теоремы затрачивались многие десятки лет упорного труда талантливых учёных. Ясно, что резкое увеличение производительности труда при доказательстве новых теорем (основанное на автоматизации) не только заметно ускорило бы темпы научного прогресса, но и дало бы возможность решать такие проблемы, которые «невооружённому» человеческому уму просто недоступны.

В настоящее время, когда автоматизация доказательств делает лишь первые робкие шаги, разумеется, преждевременно говорить о моделировании универсальных способностей доказывать теоремы во всех областях современной математики. Наиболее целесообразно на первых порах выделять относительно узкие области математики, составлять отдельные программы доказательств для каждой из них. Первые шаги в этом направлении уже сделаны. Так, известный математик Хао-Ванг, работающий в настоящее время в США, разработал программу, при помощи которой универсальная электронная цифровая машина за несколько минут доказала около четырёхсот теорем из известного труда по математической логике «Principia Mathematical. Эта программа открыла путь к доказательствам и новых, никем ранее не доказанных теорем математической логики. В Институте кибернетики АН УССР разработана программа для доказательства или опровержения произвольных теорем относительно корней вещественных полиномов (на основе так называемого алгоритма Тарского).

Положение, однако, осложняется тем обстоятельством, что далеко не для всех областей современной математики оказывается возможным построить универсальные алгоритмы доказательства или опровержения всех теорем, какие только можно сформулировать в рамках данных областей. Отсутствие подобного, так называемого универсального разрешающего алгоритма доказано, например, для арифметики натурального ряда чисел. В силу знаменитой теоремы Геделя в арифметике натуральных чисел можно сформулировать такие теоремы, которые нельзя ни доказать, ни опровергнуть!

Этот результат кажется на первый взгляд весьма мало обнадёживающим с точки зрения перспектив автоматизации доказательства теорем. Однако в действительности дело обстоит вовсе не так плохо. Дело в том, что и человек не может «запрограммировать» у себя в мозгу (в результате процесса обучения) бесконечное число методов, необходимых для установления истинности или ложности всех теорем в неразрешимых теориях (т. е. в таких теориях, в которых отсутствует универсальный разрешающий алгоритм). В результате даже самый изощрённый математик при поисках доказательства теорем в неразрешимых теориях пользуется фактически не универсальными, а частными разрешающими алгоритмами. Хотя эти алгоритмы и не способны дать ответы на все вопросы в рамках рассматриваемой теории, они тем не менее на практике дают обычно хорошие результаты. Программируя эти алгоритмы, мы решаем задачи автоматизации доказательств в неразрешимых теориях, если не в принципиальном, то, во всяком случае, в практическом аспекте.

Необходимо подчеркнуть, что механизм получения логических следствий из известных результатов, являющийся основой автоматизации доказательств, хорошо известен и может быть относительно просто запрограммирован. Однако само по себе это не может обеспечить действенную автоматизацию, так как приводит, как правило, к столь большому перебору различных возможных вариантов поиска доказательства, что такой перебор оказывается недоступным даже для современных электронных цифровых машин, выполняющих сотни тысяч операций в секунду. Главная задача в построении доказывающих алгоритмов состоит поэтому в уменьшении перебора на основе более глубокого проникновения в методы математического мышления и особенно той его части, которую принято называть математической интуицией.

Здесь напрашивается аналогия с шахматной игрой. Набор фактов, с которыми математик имеет дело на каждом этапе доказательства теоремы, аналогичен шахматной позиции, а правила логики, при помощи которых выводятся следствия из известных фактов, аналогичны правилам, по которым ходят шахматные фигуры. Придерживаясь одних лишь последних правил, практически невозможно прийти к выигрышу в партии, насчитывающей несколько десятков ходов, точно так же при помощи одних лишь правил логики практически невозможно доказать сколько-нибудь сложную теорему. И в том и в другом случаях препятствием на пути к успеху будет необходимость рассмотрения слишком большого числа вариантов. Поэтому приходится ставить промежуточные цели, достижение которых возможно за меньшее число ходов (шахматных или логических соответственно).

В шахматах постановка подобных целей определяется стратегическими правилами, основанными на оценке позиций. Что же касается теории доказательств, то в отличие от шахмат соответствующие правила здесь не сформулированы даже в первом приближении.

Потенциальные возможности автоматизации имеются и в других областях научного творчества, в частности, в постановке новых проблем и в построении новых теорий, обобщающих совокупность фактов. Однако в этом направлении сделано пока ещё столь мало, что соответствующие проблемы можно считать лишь поставленными.

Несмотря на всю важность чисто алгоритмического подхода к проблеме автоматизации научного творчества, нельзя не отметить известной его узости. Дело в том, что при таком подходе исключается возможность проявления какой-либо случайности при формировании ответа. Вне рассмотрения оказывается и такое важное свойство мозга, как способность совершенствовать свои ответы в процессе работы, по мере накопления опыта. Можно, однако, так расширить понятие алгоритма, что оно будет включать в себя как алгоритм со случайными переходами, так и самосовершенствующиеся системы алгоритмов. Такие алгоритмы в широком смысле слова могут столь же успешно программироваться и выполняться универсальными электронными цифровыми машинами, как и рассматривавшиеся ранее алгоритмы в узком смысле слова.

МОДЕЛИРОВАНИЕ ПРОЦЕССОВ РАСПОЗНАВАНИЯ ОБРАЗОВ

Следует отметить одно принципиальное отличие самосовершенствующихся систем автоматизации доказательств от систем, использующих жёсткие, неизменные алгоритмы. Если такие системы рассматривать как изолированные, не взаимодействующие с внешней средой, то возможность самосовершенствования не вносит ничего принципиально нового. То же самое будет и тогда, когда воздействия внешней среды на систему могут рассматриваться как результат работы некоторого алгоритма. В случае же «неалгоритмической» внешней среды положение существенно меняется. Для самосовершенствующейся системы алгоритмов, взаимодействующих с подобной средой, может оказаться возможным, например, доказательство (за бесконечное время) всех истинных теорем какой-либо неразрешимой теории, что заведомо невозможно для любой жёсткой системы алгоритмов.

Практически необходимость перехода к самосовершенствующимся системам возникает обычно в том случае, когда трудно найти жёсткий алгоритм, решающий заданную проблему, а алгоритм нахождения требуемого алгоритма является хотя и весьма трудоёмким, но простым с точки зрения его описания. В таком случае программируется не сам рабочий алгоритм, а алгоритм поиска или уточнения рабочего алгоритма. Задача же фактического нахождения рабочего алгоритма (и последующей работы по нему) поручается при этом машине.

Классический пример подобной ситуации – это задача распознавания зрительных образов. Если попытаться найти алгоритм (систему правил), позволяющий отличать женские лица от мужских, то нетрудно убедиться, что эта простая на первый взгляд задача оказывается в действительности очень сложной. Между тем человеческий мозг относительно легко справляется с этой задачей, но, разумеется, подобная лёгкость появляется лишь в результате более или менее длительного процесса приспособления зрительного центра, происходящего в раннем возрасте.

Естественно попытаться моделировать указанный процесс приспособления, основываясь на тех или иных гипотезах относительно механизма подобного приспособления. К настоящему времени предложено много моделей такого механизма. Все эти механизмы в более или менее явной форме используют идею запоминания одного или нескольких изображений каждого класса изображений в качестве эталонов для всех классов. Новые изображения сравниваются с эталонами и в зависимости от их близости к тем или иным эталонам относятся к соответствующему классу.

В Институте кибернетики АН УССР разработана и построена специальная приставка к универсальной электронной цифровой машине – так называемый универсальный читающий автомат. Эта приставка позволяет вводить в машину произвольные рисунки с учётом не только черных и белых полей, но и различных полутонов. Благодаря наличию универсальной цифровой машины становится возможным быстрое моделирование и опробование различных способов распознавания образов, включая системы с самосовершенствованием и самообучением. В настоящее время разработан и испытан целый ряд таких систем. Некоторые из них, например, система, обучающаяся распознаванию геометрических фигур, довольно хорошо имитируют приспособительные функции мозга человека в части такого вида деятельности.

В связи с проблемой обучения распознаванию зрительных образов заслуживает внимания специальная алгоритмическая схема для решения указанной проблемы, которая была предложена американским учёным Ф. Розенблаттом. Эта система, названная перцептроном, включает в себя, помимо чувствительных элементов (сетчатки), которые воспринимают изображение, некоторое множество довольно грубых моделей нейронов, связанных с сетчаткой случайным образом. Часть входных каналов нейронов является возбуждающими, а часть – тормозящими. Когда суммарное возбуждение нейрона превосходит его суммарное торможение на некоторую пороговую величину, нейрон возбуждается и передаёт некоторую величину, называемую весом нейрона, на специальное устройство, суммирующее веса всех подключённых к нему возбуждённых нейронов. Таких сумматоров имеется несколько, и нейроны делятся на несколько групп, в соответствии с тем, к какому сумматору они подключены.

Показание каждого сумматора интерпретируется как «степень похожести» показываемого перцептрону изображения на образ (класс изображений), заранее поставленный в соответствие данному сумматору. Специально введённый в схему перцептрона механизм поощрения увеличивает вес тех нейронов, которые возбуждаются изображением, относящимся к тому же образу, что и соответствующий этим нейронам сумматор. В противном же случае вес нейронов уменьшается. В результате моделируется некоторый приспособительный процесс: веса полезно работающих нейронов увеличиваются, а веса нейронов, которые не помогают или даже мешают правильной работе перцептрона, уменьшаются. Продолжая подобный процесс обучения, можно добиться, чтобы перцептрон научился правильно классифицировать изображения по заранее определённым группам (образам).

Возможен и несколько видоизменённый режим работы перцептрона (называемый режимом самообучения), при котором группировка изображений, к которой нужно стремиться, не задаётся заранее, а определяется перцептроном в процессе работы.

Проведённое автором теоретическое изучение работы перцептрона показало, что применённая в нём организация процесса обучения и особенно процесса самообучения далеко не всегда приводит к хорошим результатам. Многие важные черты, свойственные обучению и самообучению человека (применительно к задаче распознавания образов), отражены в схеме перцептрона плохо либо совсем не отражены. В настоящее время есть возможность гораздо более рационального моделирования тех процессов, на которые был рассчитан перцептрон. Некоторые из этих возможностей уже нашли своё воплощение в реальных программах, разработанных и опробованных в Институте кибернетики АН УССР и в ряде других институтов.

В целом работы по моделированию процессов распознавания образов развиваются в настоящее время достаточно быстрыми темпами. В первую очередь это касается зрительных образов и в меньшей степени – речевых сигналов. А ведь работа по распознаванию такого рода образов составляет значительную долю (хотя и выполняемую обычно бессознательно) работы человеческого мозга, что видно хотя бы из сравнения объёмов зрительного и слухового центров с другими участками мозга.

ОПЫТЫ ОБУЧЕНИЯ МАШИН

В последнее время идеи самоорганизации и самосовершенствования начинают вторгаться и в процессы моделирования таких видов умственной деятельности, как логическое мышление, обучение языку и т. п. Особый интерес представляют семантические построения, обеспечивающие автоматизацию распознавания смысла и обучения такому распознаванию. Опыты такого рода были успешно проделаны в Институте кибернетики АН УССР в Киеве.

Первоначальная идея автора, положенная в основу автоматизации процесса обучения распознаванию смысла фраз, состояла в следующем. Предположим, что рассматриваются лишь такие фразы, которые имеют простейшую грамматическую конструкцию, а именно подлежащее – сказуемое. Пусть далее дан какой-либо набор существительных и глаголов, из которых будут составляться подобные фразы. Первоначально некоторый набор фраз указанного типа составляется человеком (учителем), причём при их составлении ограничиваются лишь такими фразами, которые, по мнению учителя, имеют смысл. Эти фразы одна за другой вводятся в машину и запоминаются ею.

Процесс запоминания организован таким образом, что вначале машина осуществляет «голую зубрёжку» осмысленных фраз, т. е. запоминает их без всякого изменения. Однако при известных условиях характер запоминания изменяется. Это происходит тогда, когда число фраз с одним и тем же сказуемым превосходит некоторую фиксируемую заранее величину – так называемый коэффициент терпения.

Пусть, например, коэффициент терпения равен двум, а машине после двух осмысленных фраз «профессор думает» и «студент думает» была сообщена новая осмысленная фраза «мальчик думает». В таком случае машина, вместо того чтобы зазубрить эту новую фразу, вводит новое понятие для обозначения класса всех думающих и запоминает, что профессор, студент и мальчик относятся к этому классу.

Подобная перестройка характера запоминания не приводит пока ещё к появлению у машины каких-либо новых сведений о множестве всех осмысленных фраз по сравнению с тем, что сообщил ей учитель. Принципиально иной эффект достигается введением нового процесса, называемого процессом экстраполяции осмысленности. Этот процесс также управляется неким коэффициентом, называемым коэффициентом осторожности. Для того чтобы понять сущность указанного процесса, предположим, что коэффициент осторожности равен двум, а машиной уже образован класс думающих. Если теперь машине сообщить, что два каких-либо представителя класса думающих, скажем, профессор и мальчик, могут также говорить, то машина экстраполирует заключение, что все думающие являются вместе с тем и говорящими. В результате машина делает правильный вывод, что фраза «студент говорит» является осмысленной фразой, хотя бы она и не содержалась в числе осмысленных фраз, на которых было проведено обучение машины.

Разумеется, в результате описанного процесса экстраполяции осмысленности машина может прийти и к неверным выводам. Если бы, скажем, в уже рассмотренном примере первоначальный класс был бы образован не по признаку сочетаемости с глаголом «думать», а по признаку сочетаемости с глаголом «стоять», то в результате процесса экстраполяции машина пришла бы к неправильному заключению, что все стоящие являются вместе с тем и говорящими.

Чтобы уменьшить число подобных ошибок, перед экстраполяцией машина составляет предварительно несколько фраз с глаголом «говорить», выбирая существительные (подлежащие) из класса стоящих случайным образом. Сообщив эти фразы учителю, машина спрашивает, осмысленны ли они? И лишь получив на этот вопрос утвердительный ответ, машина производит экстраполяцию.

На основе описанной идеи в Институте кибернетики АН УССР была построена программа для вычислительной машины «Киев», при помощи которой были проведены опыты по обучению машины смыслу фраз не только простейшей, но и более сложной грамматической конструкции. Во время этих опытов машина сама создавала понятия «человек», «мебель» и др.

Интересно отметить, что, меняя значения некоторых параметров (аналогичных описанным выше коэффициентам терпения и осторожности), введённых в программу, удаётся моделировать самые различные темпераменты и типы обучения – от голой зубрёжки до склонности к крайне поспешным выводам и заключениям. Впрочем, оба этих крайних случая приводят к замедлению процесса обучения (в первом случае из-за отсутствия экстраполяции, а во втором – из-за частых ошибок и вызываемой ими необходимости перестройки классов). Существуют (находимые пока опытным путём) наилучшие значения указанных коэффициентов, при которых процесс обучения происходит в среднем наиболее быстро. Эти значения, впрочем, сильно зависят от первоначального набора слов, из которых строятся фразы.

Из-за небольшого объёма памяти машины «Киев» опыты по обучению проводились с весьма бедным словарём, насчитывающим всего около ста слов. При наличии существенно большей памяти дальнейшее развитие описанных принципов может привести к построению программ для обучения машины тому или иному человеческому языку с учётом не только его синтаксиса, но и семантики.

Для изучения возможностей самоорганизующихся систем большой интерес имеют опыты по моделированию биологической эволюции. Опыты такого рода были проделаны в Институте кибернетики АН УССР на универсальной электронной цифровой машине «Киев». Моделировался некоторый весьма просто устроенный «мир», в котором действовал «закон природы», управлявший перемещением «пищи» из одних участков этого «мира» в другие. Обитающие в описанном мире «живые существа» моделировались в виде программно реализованных автоматов.

Каждый автомат снабжается двумя счётчиками – счётчиком «жизни» и счётчиком «голода». Первый счётчик отсчитывает число моментов времени, прошедших со времени «рождения» автомата, а второй – число моментов времени, отделяющих автомат от последнего момента, когда автомат находился на участке пространства, снабжённом «пищей». При достижении счётчиком «жизни» или счётчиком «голода» некоторых определённых заранее значений автомат «умирал», т. е., попросту говоря, исключался из дальнейших рассмотрений.

Перемещения автомата в «мире» определялись его состояниями, а переход автомата из одного состояния в другое осуществлялся в зависимости от состояния ближайших к нему участков «мира» (т. е. от наличия или отсутствия в них «пищи» и других автоматов). Специальная матрица, управляющая подобными переходами, первоначально задаётся случайно, а впоследствии испытывает ещё небольшие случайные изменения («мутации») в процессе «размножения» автоматов. Был выбран простейший вид размножения путём деления, причём одна из образовавшихся половинок полностью наследовала структуру исходного автомата, а со второй происходило то же самое, за исключением случайной мутации в матрице переходов. Момент деления определялся подходящим «возрастом» автомата (показанием его счётчика «жизни»), относительно малым показанием счётчика «голода» и наличием свободных соседних ячеек для вновь образующихся в результате деления автоматов.

В результате проведённых опытов имитировался процесс естественного отбора и приспособления автоматов к выбранному «закону природы». Этот процесс может быть при желании интерпретирован так же, как процесс «познания» коллективом автоматов соответствующего «закона природы», ибо в результате естественного отбора возникают автоматы, в структуре матрицы переходов которых всё более и более отражается выбранный «закон природы». Принципиально не видно никаких ограничений для того, чтобы с помощью подобных моделей, использующих крайне простую исходную структуру автоматов, но весьма сложный процесс развития «природы», можно было бы получить весьма высокие формы приспособления к указанному процессу (вплоть до возникновения и совершенствования моделей человеческого сознания и сознательной человеческой деятельности).

И всё же в настоящее время сделаны лишь первые шаги в построении общей теории самоорганизующихся систем, как основы моделирования мыслительных процессов. Несомненно, что успехи этого направления в будущем помогут объяснить многие загадки мышления и создадут прочную базу для автоматизации сложных мыслительных процессов.